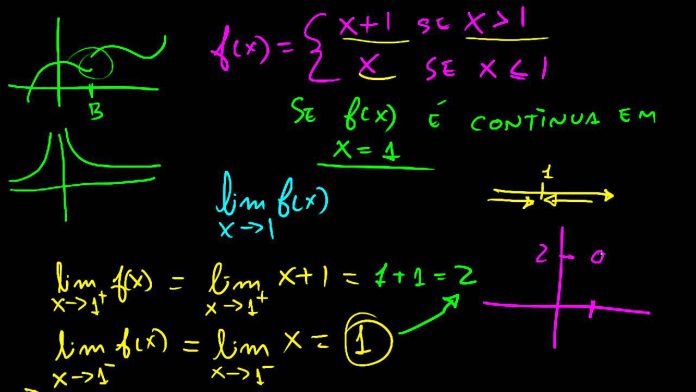
Resposta para questão: “Com relação à definição do conceito de continuidade de uma função, dizemos que uma função () é dita contínua em um ponto do seu domínio quando: a. f parêntese esquerdo x parêntese direito igual a f parêntese esquerdo a parêntese direito texto para todo fim do texto x pertence D parêntese esquerdo f parêntese direito b. lim de x sem ligadura seta para a direita a de f parêntese esquerdo x parêntese direito igual a f parêntese esquerdo a parêntese direito c. texto para todo fim do texto épsilon maior que 0 texto existe fim do texto delta maior que 0 vírgula texto tal que fim do texto linha vertical f parêntese esquerdo x parêntese direito menos L linha vertical menor que épsilon texto sempre que fim do texto linha vertical x menos a linha vertical menor que delta d. lim de x sem ligadura seta para a direita a de f parêntese esquerdo x parêntese direito não igual f parêntese esquerdo a parêntese direito e. Nenhuma das demais alternativas está correta.”
A alternativa correta para a definição de continuidade de uma função f em um ponto a do seu domínio é a b):
b. lim de x sem ligadura seta para a direita a de f(x) = f(a)
Explicação:
Definição formal:
Dizemos que uma função f é contínua em um ponto a do seu domínio se o seguinte limite existir e for igual ao valor da função no ponto a:
lim_(x->a) f(x) = f(a)
Em outras palavras, para que f seja contínua em a, o valor da função f(x) deve se aproximar cada vez mais de f(a) à medida que x se aproxima de a, por ambos os lados (direita e esquerda).
Interpretação gráfica:
Graficamente, a continuidade de uma função em um ponto significa que o gráfico da função não possui “buracos” ou “saltos” nesse ponto. Ou seja, o gráfico pode ser desenhado sem tirar o lápis do papel.
Exemplos:
- A função f(x) = x^2 é contínua em todos os pontos do seu domínio (ℝ).
- A função g(x) = 1/(x-1) é descontínua no ponto x = 1, pois o gráfico da função possui um “buraco” nesse ponto.
Considerações importantes:
- A definição de continuidade em um ponto pode ser estendida para intervalos. Uma função é contínua em um intervalo se for contínua em todos os pontos desse intervalo.
- A continuidade é uma propriedade importante em Cálculo e outras áreas da matemática. Ela é utilizada, por exemplo, para definir derivadas e integrais.
Outras alternativas:
- A alternativa a) é incorreta porque apenas define a igualdade entre f(x) e f(a), mas não menciona o limite.
- A alternativa c) define a definição de epsilon-delta de continuidade, que é uma forma equivalente à definição formal, mas menos intuitiva.
- A alternativa d) é a definição de descontinuidade, o oposto de continuidade.
- A alternativa e) é incorreta porque a alternativa b) é a correta.
Conclusão:
A definição correta de continuidade de uma função em um ponto é a b): lim_(x->a) f(x) = f(a). Essa definição garante que a função se comporte de maneira suave e contínua no ponto a.
Esta é a resposta da questão:
Com relação à definição do conceito de continuidade de uma função, dizemos que uma função () é dita contínua em um ponto do seu domínio quando: a. f parêntese esquerdo x parêntese direito igual a f parêntese esquerdo a parêntese direito texto para todo fim do texto x pertence D parêntese esquerdo f parêntese direito b. lim de x sem ligadura seta para a direita a de f parêntese esquerdo x parêntese direito igual a f parêntese esquerdo a parêntese direito c. texto para todo fim do texto épsilon maior que 0 texto existe fim do texto delta maior que 0 vírgula texto tal que fim do texto linha vertical f parêntese esquerdo x parêntese direito menos L linha vertical menor que épsilon texto sempre que fim do texto linha vertical x menos a linha vertical menor que delta d. lim de x sem ligadura seta para a direita a de f parêntese esquerdo x parêntese direito não igual f parêntese esquerdo a parêntese direito e. Nenhuma das demais alternativas está correta.
Veja mais questões em resolvida em nossa página de educação.



